This paper is available on arxiv under CC 4.0 license.
Authors:
(1) Nicolas Bernal, New York University Abu Dhabi;
(2) Partha Konar, Physical Research Laboratory;
(3) Sudipta Show, Physical Research Laboratory.
Table of Links
- Abstract and Intro
- S-matrix: Unitarity and its Consequences
- Dark Matter Annihilation and Unitarity Bound
- Low-temperature Reheating
- Freeze-out with a Low-temperature Reheating
- Summary and Conclusion
- Acknowledgments and References
4. Low-temperature Reheating
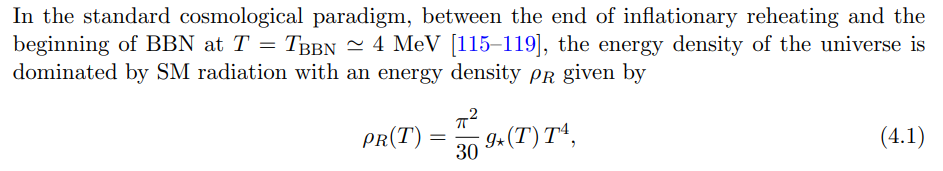
where T corresponds to the temperature of the SM bath. It follows that the Hubble expansion rate H is therefore
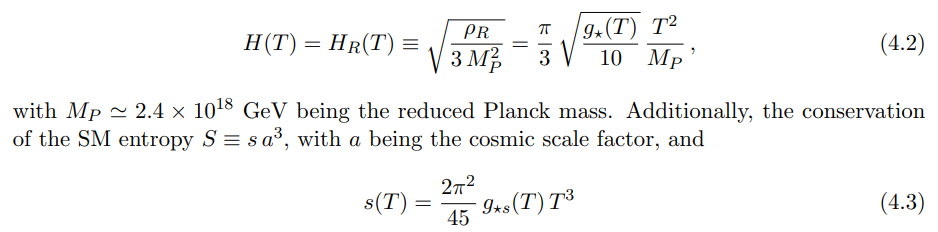
the SM entropy density implies that the temperature of the SM bath scales as
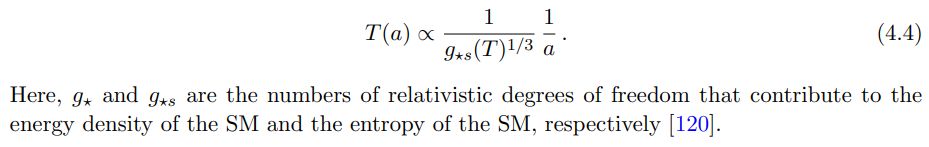
However, it is interesting to emphasize that the standard cosmological scenario is not granted and that alternative cosmologies could also have occurred [121]. In the following, we focus on cases characterized by low-temperature reheating. This reheating could correspond to the period just after the end of inflation, or to a secondary period in which an extra component beyond SM radiation dominated the energy density of the universe. In particular, two scenarios will be reviewed: one where the extra component ϕ that dominated the expansion of the universe has an energy density that gets diluted faster than radiation and does not decay (that is, a kination-like scenario), and the other where ϕ scales as nonrelativistic matter and decays into SM particles (that is, an early matter-dominated scenario). These two scenarios will be described below.
4.1. Kination-like
In this scenario, the universe was dominated by a component ϕ whose energy density redshifts faster than free radiation [113], as

with n > 0. A typical example of this scenario corresponds to kination [122, 123], where n = 2. However, larger values for n are also possible, appearing, for example, in the context of ekpyrotic [124, 125] or cyclic scenarios [126–129].

where we have taken into account that, as ϕ is not decaying, the SM entropy is conserved, and therefore the SM temperature follows the standard scaling shown in Eq. (4.4).
4.2. Early matter domination

It follows that the Hubble expansion rate is

Having settled the evolution of the background, in the next section the dynamics of the thermal DM in such alternative cosmological scenarios, and in particular the impact on the unitarity limit, will be carefully studied.
[4] It is worth mentioning that, in general, the non-adiabatic period could have been preceded by an adiabatic period with ϕ-domination, and by another era dominated by SM radiation. Here, however, we assume that the DM freeze-out happens in the non-adiabatic period so that previous stages of the universe play no role. This is true if ϕ is identified with the inflaton or simply if the nonadiabatic era is long enough.
