Authors:
(1) Omer Rathore, Department of Physics, Durham University;
(2) Alastair Basden, Department of Physics, Durham University;
(3) Nicholas Chancellor, Department of Physics, Durham University and School of Computing, Newcastle University;
(4) Halim Kusumaatmaja, Department of Physics, Durham University and Institute for Multiscale Thermofluids, School of Engineering, The University of Edinburgh.
Table of Links
Methods
Results
Conclusions and Outlook, Acknowledgements, and References
Particle Based Application
The graph representing load balancing for SPH is incredibly dense as illustrated in Figure 9a due to its fully connected nature. An optimised partition should aim to minimise the mismatch between subsets of total node weight, while also minimising the sum of cut edge weights. It is not a clear a priori which of the two objectives is more important as this is likely to be somewhat dependant on the HPC architecture, in particular whether intra or inter processor bandwidth is the more limiting factor for the CPU stack. For example, in the case of the latter, it would be more strategic to further minimise cut edge weight where possible even at the cost of a slightly higher node imbalance and vice versa for the former. Therefore in order to remain general, the task will be considered a multi-objective optimisation problem here.
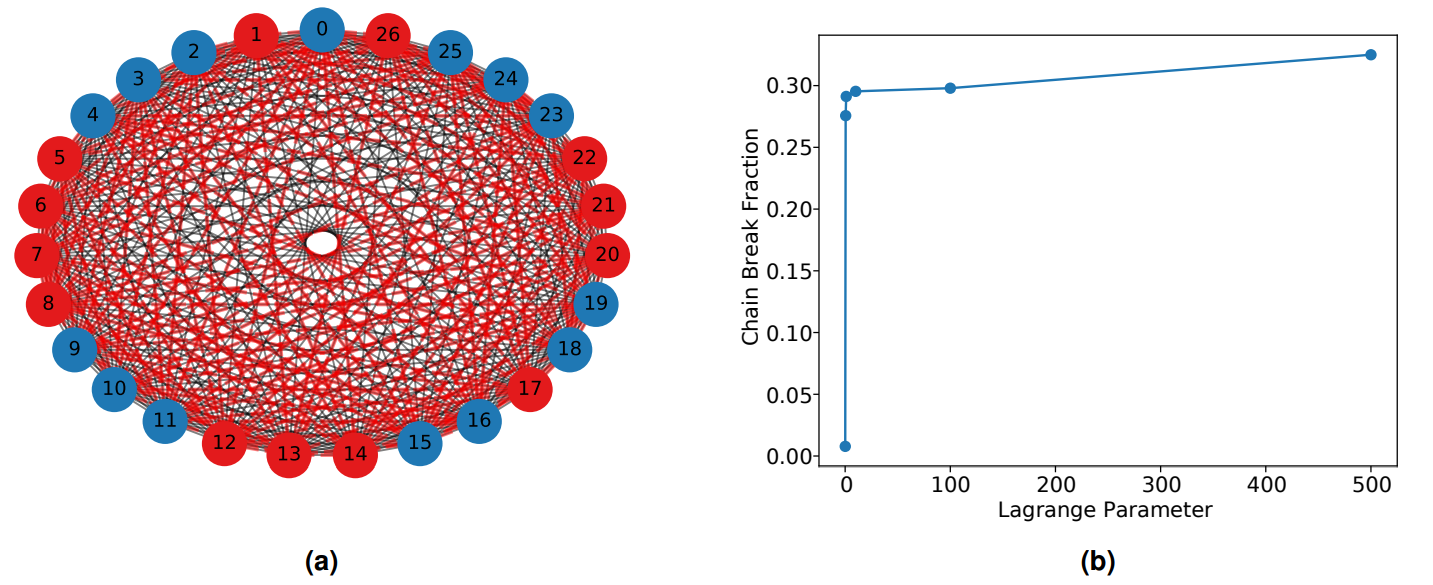
The Lagrange parameter, γ, determines the relative importance between these two objectives as shown in Equation 6. A high value implies more significance attributed to minimising the difference of node weights between the two subsets. In the limit of very large γ the problem essentially reduces back to number partitioning since the edges will have negligible relative influence. An interesting finding was that changing this parameter had an unexpected impact on the chain break fraction. This is shown in Figure 9b where a small value results in lower chain breaks than was observed in the grid based, number partitioning example even for a graph of the same size. Indeed, as the Lagrange parameter is increased, the problem tends back towards number partitioning and chain breaks become more frequent. This is despite no change to the underlying graph structure, which remains a 27 node clique. Moreover, numerical values are auto-scaled in the process of mapping onto a quantum processor and so differences in the values of weights alone should not be significantly impacting chain breaks. This implies that despite not changing the nature of the underlying embedding, the load balancing problem here is intrinsically more resilient to chain breaks than for its grid based counterpart.
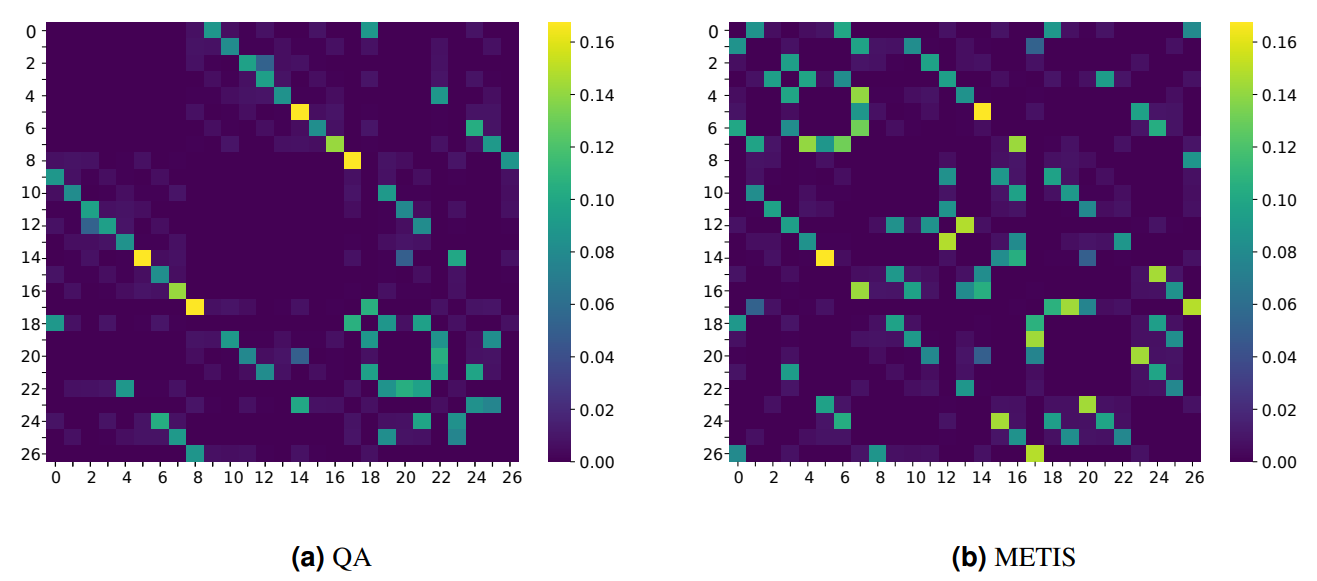
Consider for now a neutral value for the Lagrange parameter of unity. A single QA was conducted with one thousand anneals and the lowest energy solution compared to a partition obtained using METIS, a state of the art classical graph partitioning software. This is illustrated in Figure 10, which displays the cut edge matrices as heat maps. Each entry in the matrix represents the edge connecting nodes with the corresponding axis indices, while the color intensity is indicative of the weight of said edge. A color value of null (i.e. dark purple) indicates that edge was not cut. Both QA and METIS make an exact total of 182 cuts each and share the same magnitude in terms of single largest cut. However, QA consistently makes better choices in exploring the energy landscape and manages to sever less expensive edges for a combined saving of close to 33%. The combined weight of cut edges from this QA run was only 66% the size of its METIS counterpart. Furthermore, this came with a better node balance as well where the degree of imbalance using QA was only 34% the size of imbalance allocated by METIS.
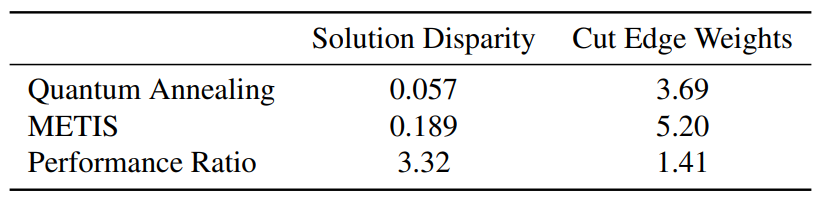
Repeating the QA runs five times and averaging, the same trend still stands as indicated in Table 1, suggesting a resilience of the method to probabilistic fluctuations. Note that node and edge weights have been normalised by the same factor for both methods as they operate on the same data set. Furthermore the “Performance Ratio” entries in the table are simply the fractional result of dividing the corresponding METIS entry by the QA counterpart. As both objectives are tailored to be minimised, a larger than unity performance ratio indicates some quantum advantage. Moreover QA performs better across both objectives simultaneously.
In addition to this, the outcomes of quantum annealing can be further fine-tuned to meet the specific needs of the HPC cluster by adjusting the Lagrange parameter. To maintain a broad applicability, this study extensively explored the parameter’s state space through 100 iterations with 1000 anneals each and evenly spaced values for the Lagrange parameter between 0 and
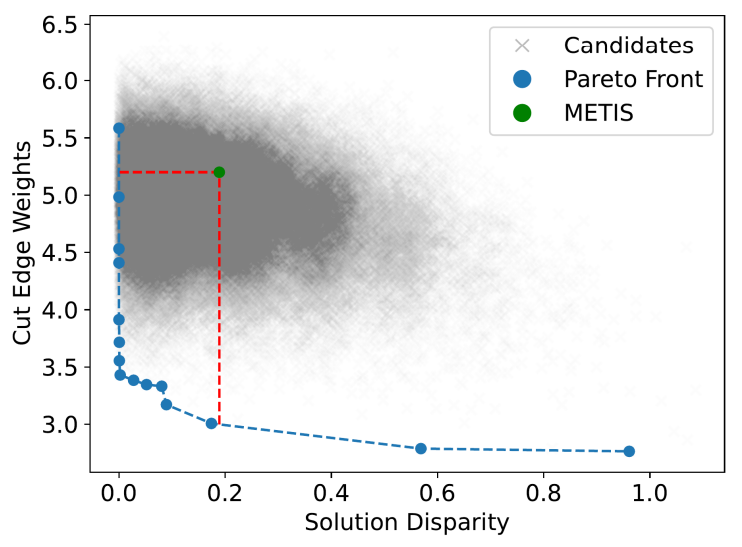
50. The Pareto dominant solutions in terms of the two objective functions obtained from this process are presented in Figure 11. The Pareto front here represents a set of solutions for which one objective function cannot be improved without bringing about a detriment to the second objective. The right side of the Pareto front is fairly close to horizontal, suggesting that if one approaches from the far right, vast improvements can be made in terms of solution disparity at the cost of a very minimal increase to cut edge weights. Conversely, initially starting at the left and proceeding towards the right large improvements to the cut edges are attainable at little cost to the node balance. The solution from METIS is also included for comparison and evidently inferior in that it is clearly possible to improve both objectives. Moreover the latter is true not just for a handful of lucky anneals, but for a large proportion as observed with the collection of QA points that lie off of the Pareto front but still are Pareto dominant in relation to the METIS output. This corresponds to close to 41000 of the total 100,000 sample solutions and demonstrates the resiliency of QA for complex problems. Even outside this region, most candidate solutions are only inferior to METIS in one objective, likely as a result of enforcing either very large or very small Lagrange parameters. This will naturally prioritise one objective even at the potential detriment of the other.
This paper is available on arxiv under CC BY 4.0 DEED license.

