Authors:
(1) Kun Lan, University of Science and Technology of China;
(2) Haoran Li, University of Science and Technology of China;
(3) Haolin Shi, University of Science and Technology of China;
(4) Wenjun Wu, University of Science and Technology of China;
(5) Yong Liao, University of Science and Technology of China;
(6) Lin Wang, AI Thrust, HKUST(GZ);
(7) Pengyuan Zhou, University of Science and Technology of China.
Table of Links
3. Method and 3.1. Point-Based rendering and Semantic Information Learning
3.2. Gaussian Clustering and 3.3. Gaussian Filtering
4. Experiment
4.1. Setups, 4.2. Result and 4.3. Ablations
3. METHOD
Given a well-trained scene using 3D Gaussian representation, scene rendering images, and corresponding camera parameters, we initially employed an interactive 2D segmentation model [23] to segment the rendered images. Then, the obtained 2D segmentation maps are used as guidance to facilitate the learning of semantic information (object code) added to the 3D Gaussians. Finally, we use KNN clustering to address issues of semantic ambiguity in certain 3D Gaussians, while optional statistical filtering can help eliminate those 3D Gaussians that have been erroneously segmented. The pipeline is depicted in Fig. 1.
3.1. Point-Based rendering and Semantic Information Learning
Gaussian Splatting [1] employs a point-based rendering technique (α-blending) to render a 3D scene onto a plane, and the color of a pixel on the plane can be calculated as:

To achieve segmentation of a 3D scene, semantic information needs to be incorporated into the representation of the scene. Inspired by 2D segmentation, we assign an object code
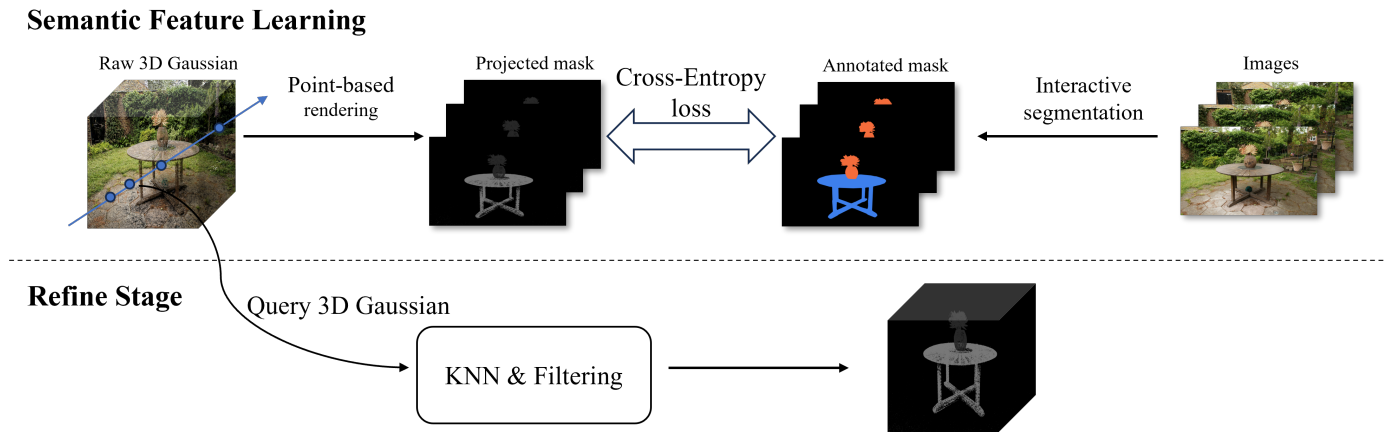

To use 2D segmentation maps as supervision for learning the added 3D semantic information, it is necessary to project the added semantic information from 3D onto a 2D plane. Inspired by α-blending, we consider the pixel categories in the rendered 2D segmentation map as a weighted sum of the categories of multiple 3D Gaussians along the current ray during rendering. We assume that the first 3D Gaussian contributes the most, with each subsequent 3D Gaussian’s contribution diminishing in accordance with its distance from the rendering plane, and this contribution is also proportional to the size of the 3D Gaussian itself. The category of each pixel on the rendered image can be represented by the object code of o the 3D Gaussians as:
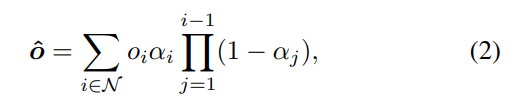
which simply replaces the color c of each 3D Gaussian in Eq. (1) with the object code of each 3D Gaussian.

This paper is available on arxiv under CC 4.0 license.
